作家:丘成桐,清华大学讲席拔擢,求真书院院长,北京雁栖湖应用数学研究院院长户外 sex,好意思国科学院院士,中国科学院外籍院士;菲尔兹奖、克拉福德奖、沃尔夫奖、马塞尔·格罗斯曼奖得主。
2022 年 9 月 22 日,丘成桐院士受邀参加“东谈主文清华”讲坛,评释《学“问”》,以下为整理并由丘先生增补后的演讲稿全文,刊登于《数理东谈主文》(订阅号:math_hmat),未经许可,不得转载。
今天,我很委宛能够在这里与群众整个商榷作念常识的经由。1979 年,我第一次归国,到今天差未几 40 多年,与好多中国数学家、科学家搏斗,遭遇了好多很好的一又友、学生,同期尽我最大的尽力培养华东谈主数学东谈主才。最近十年来,我花了不少功夫在清华大学,遴聘了一批天下第一流学者加盟。我很委宛的看到,中国的数学和基础科学百废具兴,这几年有了很大发展。一个很紧要的事情我永恒但愿跟我的共事、学生们共享,那等于,中国数学和基础科学的出路到底该若何走。
咱们要走的是一个很好的所在,是能够指导全天下数学和基础科学走向的所在,才算得上天下第一流。假如咱们作念常识都是随着东谈主家背面走,永恒不成经管紧要的问题。咱们遭遇的所谓“卡脖子”的问题,恰是因为在好多紧要问题上,照旧随着别东谈主走。原创者,在我方创作的基础上跳跃前进相比容易;至于非原创者,一般来说,只可够在他东谈主创作的基础上改变少量点,走得不远,恶果不得不受制于东谈主。
今天我想花点功夫跟群众商榷,什么是第一流的常识,卓越是第一流的常识在数学限度是如何产生的。
什么是学与问?
首先,咱们要晓得,常识有两个部分,一个是“学”,一个是“问”。这个问题两千多年前孔子就说:“学而不念念则罔,念念而不学则殆”。念念考其实等于问,念念考与问问题差不了太远,要问就必须念念考,念念考就会淡漠问题,这是分不开的。咱们中国东谈主学习很好,考试考得很好,高考考出很高的分数,以致奥数也阐述得很好。咱们学习别东谈主淡漠来的各式花式和技巧,考验的很熟,再去讲述别东谈主问出来的问题。这很好,示意咱们很有智商。然而,只是善于答题,对于常识、对于科学、对于数学的发展来说,能产生多大的孝敬呢?可惜,孝敬并未几。咱们随着东谈主家背面走,经管东谈主家淡漠的问题,这些问题也不见得是大问题,而是小问题。咱们天然无间地得回奥数金牌,然而还莫得能够出现一多数经管信得过伟大的数常识题的学者。因此,咱们一定要晓得到底如何作念常识,如何作念一流的常识,这亦然我今天要讲的要点。我也会讲几个例子,但愿群众能够感受到我的想法。
其次,作念常识除了“问”除外,还要辛好学习。学习是一个很紧要的事情,莫得基本器具,光靠念念考莫得用。孔子说“念念而不学则殆”,等于说只念念考不学习,是远远不够的。从希腊到今天,数学科学的发展已经有 2500 年的历史,在这中间有好多颇具天资,以致可以称之为天才的大数学家,他们积攒了好多了不得的常识。从当年希腊伟大的数学家欧几里得、毕达哥拉斯、阿基米德,到自后的费马、笛卡尔、牛顿、高斯、欧拉、拉格朗日、黎曼、希尔伯独特,都是六合古今少有的伟大学者。他们为什么能够千古留名呢?因为是他们一层一层地将数学这幢大厦搭建得越来越高。无论咱们天分有多好,有多擅长念念考,咱们的常识、创造力都必须以他们的常识为基础。例如,就算是一个平方的工程学家,也不可能无谓微积分。微积分等于从阿基米德阿谁时候逐步发展,由牛顿、莱布尼茨最终完成。咱们莫得目的跳跃,每一步都必须竖立在前东谈主常识的基础上。辛勤是必不可少的,咱们要学习伟大学者的常识,打好基础,技艺赓续上前走。牛顿讲谈:“要是说我看得比别东谈主更远些,那是因为我站在巨东谈主的肩膀上”。这十足不是谦善汉典。牛顿作念的好多东西,先前的科学家、数学家曾经斟酌过,只是莫得他斟酌的这样完好,后世就不再说起了。事实上,牛顿的责任都是在前东谈主的基础上作念出来的。今天,咱们要指导天下常识的潮水,非将前东谈主的常识学好不可,辛勤是十足紧要的。我这几年来一直讲数学史,等于但愿群众晓得常识的是如何传承下来的。
为什么要问问题?
“寻天东谈主乐处,拓长时心怀”,这是我父亲写的对子,我作念了少量修改。究其根源,咱们所作念的常识,尤其科学和数学上,都与大天然有很密切的关联,咱们要在追寻大天然好意思妙的经由中,找到它最故有趣有趣、最有乐趣之处,从而对大天然有深入的了解。假如咱们不了解、不抚玩大天然的好意思妙与乐趣,常识是永恒作念不好的,这等于“寻天东谈主乐处”。“拓长时心怀”是说,作念常识不单是为了高考、为了拿奖、为了作念院士、为了拿诺贝尔奖金,而是但愿所作的常识能够在科学史上留住紧要的轨迹。咱们今天读诗经、楚辞以及李白、杜甫的诗词,天然过了千年,照旧以为很故有趣有趣,能够激勉咱们的共识。他们对大天然的好意思、对东谈主世喜怒无常的态状,让东谈主以为亲切天然,这等于我说的“天东谈主乐处”。咱们作念的常识也要引起后代的共识,让他们晓得咱们今天创始的所在、发现的礼貌是何等故有趣有趣。
咱们要斟酌整个常识上前走的所在到底是什么,应该如何去意识数学的内在结构,这是许多大数学家常常念念考的问题。大常识家常常会淡漠好多问题,这少量很紧要。但中国的科学家不大爱问问题,不大问我方原创的问题,更多的是解答别东谈主的问题。天然解答的可以,但这不见得是数学和科学的真髓,紧要的是要找出我方的所在。中国最伟大的一篇讲问问题的著作是屈原的《天问》,内部问了好多问题,著作很罢休,但欠缺系统的念念维和逻辑念念考的结构,也莫得充足的器具讲述这些问题,永恒莫得完成“问”的主要精神。
《礼记·学记》说:“善待问者如撞钟,叩之以小者则小鸣,叩之以大者则大鸣。”对咱们来说,这个钟,等于大天然和万物运行的礼貌。深入的问题能够指向大天然好意思妙的深处,很快引出其它故有趣有趣的有关问题。
希尔伯特二十三问
在数学历史上,一个相等紧要的问题集,等于希尔伯特 23 问。1900 年 8 月 8 日,这位德国数学家在巴黎外洋数学家大会上作念题为《数常识题》的演讲。希尔伯特认为,从 19 世纪参加 20 世纪,淡漠一些紧要的问题,对于鼓动学科进步的作用颠扑不破。他说,一个学科能够产生大批紧要问题,技艺保持活力。他是那时最伟大的数学家,眩惑了不少东谈主听这个演讲。这 23 问基本上引颈了数学界五十年的发展。23 问不是全部由他淡漠,也有从前大数学家的问题,比如黎曼等。他将要紧的问题网罗起来,又增多了我方的问题,这是希尔伯特引颈一代风流的紧要时刻。这些问题于今并莫得全部经管,但其中部分问题的经管,就已经促发了数学学科紧要的发展。
丘成桐一百二十问
1978 年,我在普林斯顿高级研究院组织几何年卓越会议 —— 微分几何论坛,指导一批数学家、几何学家研究几何方面主要的所在。会议终末几个礼拜,我徇众条目,作为沟通的几何学家淡漠几何方面最紧要的问题。我于是淡漠了 120 个问题,天然我的问题无法跟希尔伯特 23 问等量王人不雅,但照旧很故有趣有趣。为什么我要问这些问题?因为 120 问对那时几何学遭遇的疼痛主要在什么地方进行念念考,同期指出学科上前走的所在,以及经管后会产生什么紧要的恶果和影响。这些问题到了今天,概略三分之一被经管,值得委宛的是,大部分都是正面的经管,基本印证了猜想的所在是紧要的、是正确的,好多数学家为了经管这些问题也得到了很好的恶果。我到咫尺照旧很委宛,我方作念到了这个事情。
一些好的问题短期内不见得有很大的影响力,因为需要花时期去消化,去念念考。然而,这些问题依然淡漠,常常会影响到数学中某些学科的所在。这 120 个问题促成了一个紧要的学科 “几何分析”的发端。好多好的几何学家对这些问题都有风趣,鼓动了这个学科的发展,再次印证了问问题是很紧要的事情。
然而,问题有好的,也有不好的。什么叫好的问题?好的问题等于,念念考这个问题本人,就发展出一系列的想法、催生出一系列著作。无论最终是否经管,只是推敲、研究这个问题的经由都很紧要。好的问题一般简约、很漂亮,可以经管数学上好多疑难。经管了它,所在限度里许多问题都会随之经管。这就好像在长江内部有一块巨石,将巨石挪开,水流就会顿时变得更顺畅,好的问题会让东谈主豁然轩敞。
我咫尺来讲讲当年我淡漠的 120 个问题中的两个题目,天然它们到今天还莫得全部经管,然而好多学者花了不少功夫,也得到好多紧要的发展。
能否听出鼓的面积?
我要例如的第一个问题是对于声息和几何的相干。古希腊期间,东谈主类就意识到声息由一些基本音组合而成。无论弹钢琴或是打鼓,敲击产生不同频率的波动,发出声息。波动由多个基本波组合而来,咱们上音乐课时都知谈基本音级 Do Re Mi Fa Sol。科学家对基本音级、基本波都很感风趣。每个基本波有固定的频率,频率则由鼓的谱算计得到。波动产生很漂亮的图形,底下的图片清晰了不同的波动,有高、有低,还有不动的地方。对于这样漂亮的几何,几何学家十分兴趣。

(图片来自齐集)
1966 年,凸起概率学人人 马克·卡茨(Mark Kac)指出著明的几何学家博赫纳(Salomon Bochner)提过一个问题:咱们可否听出鼓的阵势?
这一问题的念念想可以回顾至 1910 年。那时,量子力学刚刚萌芽,物理学家洛伦兹(H. A. Lorentz)在哥廷根大学演讲时,淡漠了一个有趣的数常识题:是否可以通过鼓声的谱和频率估算鼓的面积?希尔伯特对于这个问题很感风趣,但他认为这个问题太难,他豆蔻年华,不可能看到这个问题的经管。当年,希尔伯特在德国哥廷根大学培养了一大群优秀的学生,其中不少成为 20 世纪著明数学家。外尔(Hermann Weyl)等于其中之一。外尔是一位相等紧要的学者,他创始了今天高能物理中的要领场表面。过了一年,外尔就把这个问题经管了。底下这个公式自后被称作外尔公式, 是 往常总共谱的数量,除以 的幂, 越大时,极限与面积乘以一个常数一样。
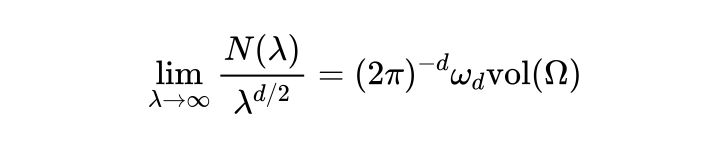
外尔经管问题的念念路和花式很紧要。他认为,谱越来越高,按照量子力学的不雅念,即谱的不雅念,可以推测到局部的几何变化,从而推出外尔方程。这是个很紧要的方程,对今天的数学仍然有紧要的影响,对于数论和几何也十分紧要。
外尔的念念路和花式还可以上前回顾。欧拉跟黎曼都是历史上最伟大的数学家,我想很少东谈主能够否定这句话。欧拉研究了一个很简陋的问题,当 是正整数时,下列式子的和是若干?
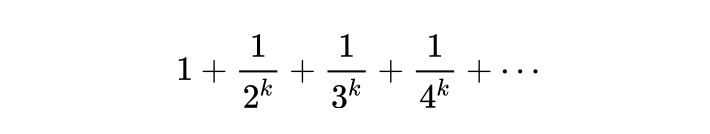
他花了好多功夫研究这个问题,产生了紧要的泛函方程。黎曼将其推行,写下了著明的黎曼函数。
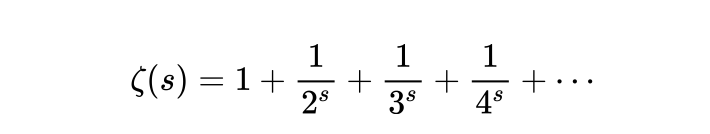
他发现这个函数十分漂亮,可以在整个复平面上界说,等于说同意 为复数。黎曼发现这类复函数具有对称性,有较明确的零点和顶点,以及不显着的零点,黎曼猜测这些不显着的零点都在一条直线上,同期这些零点的散播和素数的散播,有密切的相干。这是个划期间的责任,这个函数影响了数论的发展,也影响了外尔的责任。
外尔推行了黎曼函数的念念意料一般的空间,用以研究“听鼓声估算面积”这一问题,并最终经管。他将黎曼 函数中的整数改为谱,从而将面积与频率商酌起来。鼓声的谱越来越高,可以推知局部的几何,得出一个很紧要的论断:面积跟频率有很密切的相干。
能否听出鼓的面积 —— 这个问题由洛伦兹从物理阵势开赴,淡漠问题,最终由外尔经管。这个问题简约、天然、有趣,经管的花式激勉了几何上不少紧要的发展。
谱可以视为几何图形的量辅音讯,咱们事实上得回了量辅音讯和几何的相干。谱向无尽增大时,得到局部的几何音讯,包括曲率、面积元等; 谱小时,得到几何的拓扑或是宏不雅音讯。因此,几何学家对几何图形最小的谱也有浓厚的风趣。
要了解卡兹的问题,需要知谈总共谱的几何有趣有趣,因此经管起来更为复杂,于今莫得全部解答。
波节线的长度猜想
鼓膜振动时,不动的地方,咱们称之为波节线(nodal-line)。克拉尼实验将粉末放在鼓面上,以机器声代替鼓声,粉率先着,逐步向鼓面上不动的地方鸠合,在颠簸经由中酿成有几何有趣有趣的线和漂亮的图案。
这个实验,让咱们看到波节线的几何与谱、频率有密切的相干。频率越低、谱越高,不动的地方越大。波节线在活命中也看得到,其几何阵势变化无方,十分故有趣。比如,拍浮池在太阳光照耀下,池底酿成不同的光泽,等于波节线。波动产生波节线激勉了我的另一个念念考:高频率下波节线的长度如何变化 —— 这是我 40 多年前斟酌的一个问题。
谱函数态状鼓膜调治的阵势。每个谱,都有一个谱函数,其零点等于波节线。以下图为例:
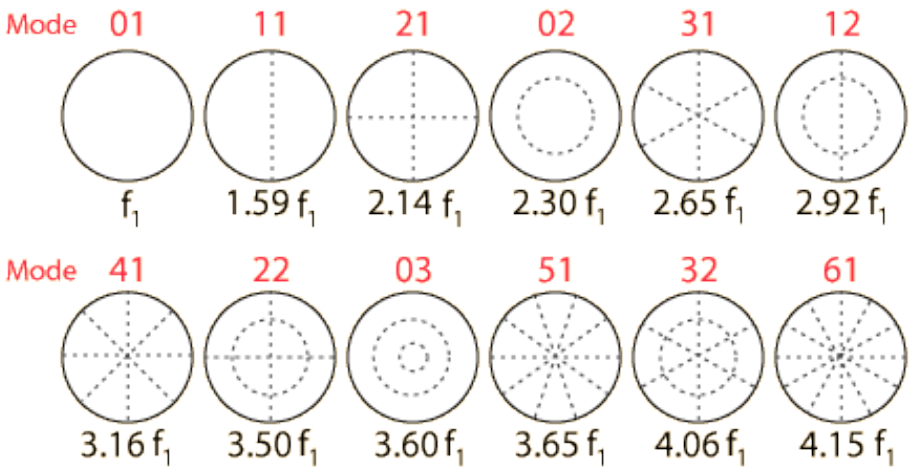
图片开端:P. Papiotis and G. Papaioannou, "Kettle: A real-time model for orchestral timpani"
第一个谱(0),变动的地方莫得零点,即莫得波节线;第二个谱(),波节线将鼓面一分为二; 箝制敲打,出现更多波节线,鼓面上不动的地方越来越多。频率越小即谱越大时,咱们不雅察到更多变化。这些变化看起来很有礼貌,只是是直线与圆形。其实,这些波叠加起来之后,波节线的几何阵势变化无意,比直线和圆形要复杂得多。
有趣的是,从克拉尼实验中,咱们可以看到,尽管波节线的图案出现好多变化,但波节线的长度似乎不太变动。1978 年,我淡漠一个问题:谱很大时,波节线的长度如何变化?我发现,打鼓时不变动的线的长度加起来,可以用谱本人的量来推测。基本上,波节线的长度跟谱成正比。我花了好多功夫淡漠这个猜想。一方面,打鼓时,波节线变化得很锐利,但长度这个基本量却变化不大。其二,我算计了好多例子,发觉其长度是在 隔邻变动的。于是得到论断:它应该知掌握述不等式。

这个不等式到咫尺限定仍然是对于波节线一个紧要猜想,引起了好多数学家、几何学家、物理学家以及数学分析研究东谈主士的良善。这个猜想,到咫尺差未几 50 年了,其中一部分被确认注解是对的,但仍然莫得全部经管。假如同学们感风趣,应当试着去经管它。这个问题很故有趣有趣,该不等式中有两个常数 C 和 c,它的几何有趣有趣十分值得咱们去摸索。
作为一个几何学家,我对洛伦兹、外尔的问题很感风趣。他们通过谱和频率的变化来估算面积,我则庄重到了鼓不动的地方有什么变化,这个猜想的念念想在好多地方都用得到。外尔的研究基于 大的情况下开展。1974 年,我启动研究当 小的时候,它和几何的相干可否描写出来,这其实是一个很紧要的问题。我在研究的时候看了好多不同的书,发现谱是量子力学中紧要的不雅念,当谱λ很大的时候,它与局部几何有很密切的相干;当谱 小时,它则跟宏不雅的几何有密切的相干。
对于极小曲面的猜想
我再来讲讲我的另一个于今还莫得经管的猜想。好多有名的几何学家都对曲面的几何有很大的风趣,他们会遴荐紧要的曲面,了解它的几何特色。极小曲面等于一个很紧要的曲面。
在三维空间或者说咱们活命的空间中,可以看到好多极小曲面。比如,在盛有肥皂水的盆里,将铁线放在水中再提拉出来,酿成薄薄的肥皂膜,等于极小曲面。

极小曲面(图片来自齐集)
在实验中,咱们使用复杂的器具,可以构造更多不同形象的极小曲面。咱们可以想象不同的肥皂泡,它们具有漂亮的几何形象。这些曲面很故有趣,我的第一个问题是:如何能找到总共完备莫得畛域的极小曲面?我在 1977 年淡漠这个问题,经过 40 年的尽力,我的同学米克斯(William Hamilton Meeks III)已经基本经管了这个问题,经管花式并不简陋,这里暂概略谈。

莫得畛域的极小曲面(图片来自齐集)
我的第二个猜想比第一个更疼痛,到咫尺还没全部经管。咱们照旧想象肥皂泡,但不在三维空间,而是在三维球中。我的猜想是,可不可以找到三维球中总共紧致极小曲面?我的一又友劳森(Herbert Blaine Lawson,Jr.)构造出一些例子,很故有趣,被称作念劳森曲面(Lawson Surface)。

(图片来自齐集)
它是一个二维曲面在三维球中的一个极小曲面;可以想象成一个肥皂泡,在封锁的三维球里出现。封锁极小曲面是一个很有几何有趣有趣的曲面,咱们几何学家热衷于了解这类曲面的性质。为什么咱们对它感风趣呢?假如将这个曲面放在四维空间的单元球里,然后从圆心取直线和这个曲面的每一个点谄媚起来得到一个三维锥,这个三维锥等于一个三维的极小流形。这些极小流形看起来似乎没什么用,但自后成为广义相对论中态状时空的紧要器具。我经管的另一个紧要问题 —— 广义相对论中的正质料猜想,主要花式等于研究肥皂泡在时空引力下如何变化。
要是把极小流形行为一个鼓面,敲击后得到一个谱,那么最小的谱等于若干?1974 年,我淡漠一个猜想,三维球中的极小曲面第一个谱 等于 。这听起来很神奇,极小曲面有好多,劳森就构建了无尽多这样的曲面。听到我的猜想,劳森吓了一跳,我跟好多一又友商榷,他们也都吓了一跳,他们问我为什么会有这样奇妙的猜测?
我认为极小曲面的第一个谱 等于 有两个紧要的事理,可以从几何的不雅念以及从谱函数的不雅念两方面来看。几何的不雅念可以说是古典力学的不雅念,谱函数的不雅念可以说是从量子力学的不雅念来看,谱跟量子力学有获胜的相干。几何不雅念认为,将极小曲面放在四维空间以后,它的坐标函数界说了一个谱函数,同期得出来的谱刚好等于 ,是以咱们得到 是这个极小曲面的一个谱,等于 。惟一的问题是,咱们不晓得 是不是第一个谱。从量子力学的不雅念来讲,咱们发觉任何曲面的第一个谱函数都有一个很紧要的性质,刚才讲波节线,即鼓不动的地方,它会将这个曲面正巧分红两部分,上述坐标函数是一个谱函数,它的零点是一个平面,假如四维空间的总共平面将咱们的曲面刚好分红两部分,那坐标函数很可能等于第一谱函数,而我的猜想就会成立。劳森构造的曲面看起来都有这种平面将曲面切两部分的性质,是以我决定这些极小曲面的最小谱等于 。
我和卡拉比先生讲了我的猜想,他认为我很有细察力。这个猜想于今仍未被确认注解。几年后,有两个数学家确认注解了三维球中的极小曲面最小的谱在 和 中间,这个谜底已经在极小曲面的研究中很有用了。

丘成桐与卡拉比
数学中的赋比兴
完成上述猜想的经由中,我的基本花式是,相比两个完全不同的不雅念,一个是几何的不雅念,一个是量子力学的不雅念,最终得出曲面最小的谱等于 ,天然还有待严格实在认注解。这种手法其实是数学研究中的习用手法。数学是很奇妙的常识,它是一个谨慎推理、讲规定的常识。咱们可以通过它们的规定和念念想来作念相比,就可以得到故有趣有趣的猜想。
诗经里讲“赋比兴”,我认为与咱们作念数学也有着很密切的相干。所谓 “比”,即用不同的景物类比,比如杨柳代表判袂或者好意思东谈主的腰枝。讲起判袂,未免想起《诗经》写谈“昔我往矣,杨柳依依。”周邦彦笔下“长条故惹行客。似牵衣待话,别情暧昧。”以及柳永的名句“杨柳岸,青灯古佛。”而说谈好意思东谈主的腰肢,则忆起张先的“细看诸处好。东谈主东谈主谈,柳腰围。”这都是缘于柳条细而柔所作的类比。更有温庭筠的“柳丝长,春雨细,花外漏声迢递。”、周邦彦描写“长亭路,年去岁来,应折柔条过千尺。”...
这万般不同的相比,亦然数学上常用的技能。数学研究者们应该斟酌这个念念路,不成只作念题目,看到数字等于数字,看到方程等于方程,它们中间有好多可以相比、可以关联之处。
好问题从何而来?
好问题从什么地方来,如何技艺经管它?咱们首先要了解不同的不雅点,就像我提到几何的不雅点与量子力学的不雅点。历史上,紧要的大常识的完成,常常是不同常识之间碰撞产生火花促成的。外尔是一个伟大的数学家,亦然一个伟大的物理学家,他在量子力学和几何学之间搭建了一个桥梁。因这个桥梁,助长出一批很好的数学家,一个全新的旅途。找到我方的所在,对咱们来讲是很紧要的事情,亦然问出好问题的紧要途径。
还有一个途径,可以产生好的问题。要经管一个大问题时,常常要有很好的器具。器具的发展是无间镌脾琢肾的经由,每个新器具又促进常识赓续发展,新器具让咱们看到不同阵势,进步咱们看待问题的深度,又促发咱们进一步发展器具。器具越多,越能产生更深刻的、更灵验的经管问题的花式。每一次器具的进步,都带动故有趣有趣的、紧要的、破裂性的常识的发展。
在伽利略期间,他看到地球是太阳系里的行星,这激勉了牛顿力学的发展。而后,东谈主类看得更远。到了 20 世纪初期,咱们了解到太阳系外还有星河系,以及不同的星云。每一次跳跃都是追随着“千里镜”这个器具无间发展的。数学上也相同如斯,咱们在经管问题时,最初的器具远远不够,还要无间发展新的器具。
费马猜想的经管亦然如斯。费马猜想距今已经有 300 多年的历史。直到 30 年前,英国大数学家怀尔斯(Andrew Wiles)才经管了这个问题。在怀尔斯之前,几百年来,大数学家们都有风趣经管这个问题。费马和欧拉就经管了 时的情形,使用了椭圆弧线的花式,得出很紧要的恶果,然而仅限于 的情形。19 世纪,德国数学家库默尔(Ernst Kummer),以为我方可以经管费马问题,恶果莫得告捷,但引入了代数中的紧要办法,即瞎想(ideal),带动经管了一多数问题,但照旧莫得压根经管费马猜想。到了 20 世纪,出现了更多不同的花式,其中一个紧要的花式,是由日本数学家谷山丰(Yutaka Taniyama)跟志村五郎(Goro Shimura),以及法国大数学家韦伊(André Weil)淡漠的谷山-韦伊-志村猜想(Taniyama-Weil-Shimura conjecture),成为经管费马猜想的紧要器具,最终由怀尔斯经管了这个 300 余年的题目。
抚玩数学之好意思的同期,我要抚玩数学好意思与真背后的礼貌。了解了它的好意思和礼貌,通过无间地相比,淡漠紧要的、具有创始性的问题。而一个学科紧要的问题,唯独在无间学习中,技艺逐步体会。
何为伟大的责任?
伟大的数学家都有一套自已对常识的看法(Philosophy),这些系统的、难懂的、极新的不雅点给陈旧的数学注入新的活力,因而产生一系列故有趣有趣的问题。正如西方歌剧《浮士德》、中国古典《红楼梦》一样,都是由不同部分构成,每个部分又自成一格,有其私有之处,但无论牡丹、绿叶,终须人人写下概要,方可将零碎的部分组合一番,成为一幅绮丽的丹青。
是以,咱们要创立一个这样的概要。在这概要的指引下,将各个不同的学科分支放在整个,技艺构建出一个宏伟的大厦!一般来说,要完成这种宏不雅的看法,并非一东谈主一时之工,一东谈主一时之问,有时长达一个世纪,才看得出这些概要的威力。1854 年,黎曼在伟大的接事演讲《论作为几何学基础的假定》中,给出了几何学的一个概要。他通过物理学中的等价道理建造了新的内蕴几何,完成了广义相对论紧要的部分。二十世纪初期,外尔拓荒李群的示意表面和要领场表面,成为当代表面物理的基础。韦伊则在上世纪定下用代数几何作为器具硏究数学的所在,完成了数学历史上一个伟大猜想 —— Weil 猜想。我的一又友朗兰兹(Robert Langlands)五十多年前淡漠著明的 Langlands 概要,用群示意表面硏究数学,产生了一多数紧要的所在和问题。这些责任可谓大气磅礴。
但凡伟大的责任,都是鼓文件,“望尽海角路”得来的恶果。我在上世纪七十年代创始当代几何分析时,主要的信念是用函数和界说的微分方程来态状空间,又通过几何来了解函数和微分方程。我淡漠的 120 个问题等于这样产生的。
何为一流的问题?
好的问题一定要有深度、有道理、而且简约。数学与文体有重复的地方。文体上,咱们通过简约的讲话态状咱们看到的阵势。数学也心爱简约。一般来讲,假如命题不够简约,则难以深入,但深入的问题也不一定很简约。总的来说,一个好的数常识题,要有深度、简约、漂亮、有趣。
什么叫深度?深度等于经管一个问题后,可以引颈新的所在,看到更真切的图景。比如,咱们爬到一个峻岭上,看到更广泛的长进和极新的邦畿。什么是简约、漂亮?在数学上,大天然的好意思景可以通过很简陋的方程解释澄澈。当年牛顿的方程、爱因斯坦方程、狄拉克方程,都是极简约的,回归了大天然之中好多很漂亮的阵势,包含了大天然的好意思妙,这天然是很漂亮的事情。文体用很简陋的讲话态状大天然的欢乐,与咱们产生心理的共识。好的数学,也能在咱们心里产生共识。当年,我听到卡拉比的讲话后,心里产生很大的震撼。我以为要是能够了解这个猜想,我将经管数学里一大片问题。
有深度的常识不一定简约,常常来需要改变。第一流的问题一定要有深度,同期本人很漂亮,很故有趣有趣,让东谈主很有风趣。庞加莱猜想、费马问题、卡拉比猜想,都是有深度、有风趣、很简约的问题,这是大问题,一流的问题。
有东谈主问我第二流、第三流的问题是什么样,我不好例如。总的来说,研究数学在于研究数学的深度、有趣有趣和本体。几十年来,咱们看到有些紧要的问题被经管了,最出名的是四色问题(Four color problem),即一张舆图只需四种神气标记就充足。这是很出名的大问题,概略 40 年前就被经管了。经管花式的终末几步,是算计机来完成的。天然,其经管花式基本正确,但咱们对这个问题本人的有趣有趣,其组合有趣有趣、几何有趣有趣,到咫尺还莫得得到深入的了解。因此,我认为这个问题其实莫得全部经管,但愿以后能够更深入地了解它,问题才算得到信得过的经管。咫尺好多数常识题,尤其是应用数学的问题,都是通过算计机算出来的,有时候可能是对的,有时候可能是不合的。这其中最大的问题是,咱们对问题的结构,对整个常识的结构并不了解,这些不成算是第一流的谜底,也不可能在工业界作念出引颈风流的一流技能。了解一个数常识题时,咱们应该深入、澄澈地了解它的结构和长进。
有一些问题,道感性比深度更大。我也作念过雷同的问题,比如我 48 年前完成的一篇小著作,那时也有很大的影响。我确认注解一个空间,曲率是大于 时,只须不是紧致的,其体积无尽大。这是一个很有趣的命题,确认注解起来也不太难。天然不算是个很有深度的问题,然而“虽小谈,必有可不雅者焉”,小谈常常可以成为大路的最先。咱们说问题只须有道理,都可以算是一个好的问题。
如何培养中国的人人?
终末,咱们谈谈如何培养人人。咱们但愿学生有视线、要用功、要提问,这都是很紧要的老师。有视线很紧要,跑到峻岭上以更广泛的视线看天下。但要是莫得爬山的器具,就只可远远的望,因此掌持器具也很紧要。70 年代,我作念了不少问题,为了经管问题,我学了好多数学,器具等于从学习中得到的,并不是应答得出来的。我看了很大批子力学的书、几何的书,从中得出了好多论断。因此,器具必不可少,不然都是泛论。我但愿群众作念常识的时候,一定要一步一步塌实的走,技艺作念出紧要的问题。但无论如何,问问题是一个最紧要的设施,问问题之后还要能够经管它,就算不成经管,也要探索出新的器具、新的所在。
今天,中国基础科学想要发展,最主要的是问问题。中国的数学家都很可以,但尚且莫得出现一批简直有智商问出紧要的问题的数学家们。咱们要老师咫尺的年青东谈主,培养他们找出紧要问题的智商。通插手问题能够产生一些紧要的器具,诈欺这些器具将问题经管之后,你的心里会很委宛。问一个故有趣的问题,同期经管它,假如经管的花式是前东谈主莫得走过的路,这个经由会更令东谈主知足,比成为天下上最豪阔的东谈主还要委宛。这是我作念常识的感念,我以为从中有很大的收成。
我本年 73 岁了,然而我这一辈子走过的路我以为很委宛。好多媒体问我,当年完成卡拉比猜想时感受如何?我援用了晏几谈的两句词,“落花东谈主独处,微雨燕双飞。”形容我当年的神志。当年我遐想经管卡拉比猜想的时候,事实上莫得东谈主同意这个猜想是对的。到了落花恶果的时候,等于我终于经管它的时候,我我方一个东谈主独巧合完成它、抚玩它,以为很散逸。所谓“微雨燕双飞”是说,在微雨之中抚玩我完成责任,以为我方与大天然交融在整个。我作念的图形,我抱有的想法与大天然相融。
三级片在线观看我想,作念好常识的学者都有这个想法,好的数学完成了以后让东谈主以为知足。这不是孤高,就像画家完成一个漂亮的丹青之后的心绪。我鼓舞年青的学者,好好的想,学好的常识,问好的问题,为了探索大天然的好意思妙尽力,为了寻找大天然中的礼貌,探讨常识,很快就会产生一多数第一流的学者。
今天就讲到这里,谢谢!
(牛芸、桂延智、王一婷 整理)户外 sex

